How does the brain work? While neuroscience provides insights on small-scale processes and overall behavior, we don’t know much for sure about the learning and processing algorithms in between. In this blog post, I will give an introduction to what we know. Let’s take an engineering perspective and play evolution: How would we build the brain under evolutionary constraints such as energy consumption, available materials and similarity to predecessors? It is hard to know for sure whether a particular evolutionary explanation is really the driving force, and although I try to cover important design options, the ones given below are in no way exhaustive, and should instead be treated as a source of inspiration for your own thoughts.

We know that the brain processes information in order to increase the chance of survival through intelligent behavior. While computers have a different purpose than their own survival, namely serving us, they also process information. Despite these different goals, let’s ask: How would a computer work if it had evolved biologically? Why would the design of a brain differ from that of a computer?

Before we dive in: This post is based on the book Neurophysiology by Roger Carpenter and Benjamin Reddi. Whenever only a page number is given as a reference, it refers to that book. I highly recommend it if you are interested in neuroscience and look for a conceptual overview.

Computers

Modern computers mainly consist of transistors as elementary processing units and wiring in between. A transistor is a switch that enables or disables conductivity of wire through a voltage, using a semiconductor material. Combining these allows to implement logical (and, or, not, …) and arithmetic operations (addition, multiplication, …), which are used as building blocks for programs, as well as memory cells. Integrated circuits contain large quantities of microscopic silicon-based transistors, connected via tiny aluminium conductors.\(^↗\) Over longer ranges, information is transmitted via copper conductors, either in form of conductive tracks on printed circuit boards and isolated cables between components.

In comparison, how do the fundamental parts for transmission and processing in the brain work?

Long-range transmission

I will start with the question how long-range transmission could be designed.

Chemical

Non-electrical, chemical transmission of information is sufficient for small animals with only a few cells but fails to scale due to low diffusion speeds. Delays can be reduced by circulation such as blood flow, but even then render this approach impractical for time-critical survival activities such as fight or flight. Because all cells along the path of transmission receive the same chemicals, the number of different messages is limited by the number of types of chemicals and receptors, resulting in low specificity.\(^{\text{↗ pp. 3-4}}\) Hormonal transmission is still useful for slow broadcasts, and we observe several hundred types of hormones in humans \(^{\text{↗ p. 4}}\), for example regulating digestion, blood pressure and immune response.

Electrical

Brains did not evolve isolated metal conductors and transistors. One reason could be that arranging metal and semiconductor materials and integrating it with existing biological structures might be hard, but there could be stronger arguments as discussed later.

Brains are based on cells and it is evolutionary straight-forward to use those as conductors with the cell membranes as isolation. The problem is that this yields very bad conductors for the following reasons:

It is fun to see that extracellular fluid is similar to diluted seawater, which is where cells evolved first:

Ion concentrations (mmol/kg)	Seawater \(^↗\)	Extracellular Plasma \(^↗\)
Cl⁻	546	100±5
Na⁺	469	140±5
K⁺	10.2	4.2±0.8
Ca₂⁺	10.3	0.75±0.25

The free ions cause high conductivity which makes isolation an important issue. Cell membranes have a specific resistance about a million times lower than rubber. \(^{\text{↗ p. 20}}\)

The fluid in the core of nerve fibers has a specific resistance about 100 times higher than copper. \(^{\text{↗ p. 20}}\)
With a typical diameter of 1µm \(^↗\), nerve fibers are about 1000 times smaller than copper cables. While shrinking the diameter by a factor of 1000 causes the leaking surface area to shrink by a factor of 1000, it also means that the cross section areas is a million times smaller, making the situation worse.

In a leaky conductor, voltage and current decay exponentially with distance from the start, as the leaking current is proportional to the current itself. How good such a conductor is can be specified through the length during which the voltage drops to \(\frac{1}{e}≈37\%\) of the initial voltage, called space constant. It turns out that for a given length \(\Delta x\) of wire with conductor resistance \(R_c\) and isolation resistance is \(R_i\), the space constant is \(\lambda = \sqrt{\frac{R_i}{R_c}} \Delta x\). From the observations above we can conclude that \(\frac{R_i}{R_c}\) is roughly \(10^6 \cdot 100 \cdot \frac{10^6}{1000} = 10^{11}\) times smaller compared to a copper cable, making \(\lambda\) more than 100000 times smaller. To improve things by a bit, evolution invented myelination, wrapping fatty, isolating cells (called glial cells) around nerve fibers in order to increase \(R_i\). Still, a myelinated frog nerve fiber with a large diameter of \(14µm\) only has a space constant of about \(4mm\).\(^{\text{↗ p. 20}}\) Comparing that to the hundreds of kilometers for a phone wire, we can conclude that cells are pretty bad conductors. This is a serious problem for long-range transmission, as it makes a signal indistinguishable from noise after a very short distance.

Side note: Myelination also has the effect of reducing capacitance \(C_i\) as distance between inside and outside is increased. This results in less charge being diverted into the capacitance resembled by the membrane, resulting in faster transmission velocity, which turns out to be proportional to \(\sqrt{\frac{1}{R_c R_i C_i^2}}\), often expressed as \(=\frac{\lambda}{\tau}\), where \(\tau=R_i C_i\) is called time constant.\(^{\text{↗ p. 42}}\) \(^{\text{↗}}\)

Designing amplifiers

We can try to extend the range by amplifying signals at regular intervals. Because we need many of these repeaters for longer distances with each one adding some noise, after some distance it will be impossible for the receiver to know what the original strength of the signal was. How can we still transmit information? We could use a protocol that only cares about whether a message was sent or not. To keep the repeaters from amplifying noise, they need a mechanism to only trigger above a certain threshold. On the other hand, to keep the signal from being dropped, we need to make sure that amplification is strong enough to trigger the next repeater. How can we design such repeaters? A fundamental property of this approach is that it will take energy to amplify the signal on the way, meaning that any design will need a power source for amplification, comparable to how amplifier circuits have an electric power source.

How do we implement such a thresholded amplifier? One possibility would be to pump charge from the outside of the cell into the fiber whenever a signal above the threshold is detected, thereby increasing the current in the fiber. This would mean that an ion pump would have to work in sharp bursts to react quickly enough, which might be problematic: We would need either a very flexible energy supply or local storage making it hard to rely on established mechanisms such as ATP-ase. How can we fix this? Instead of pumping in ions on activation, we can pump out ions beforehand, and let them passively rush in when we detect a signal by opening up ion channels. That solves our problem very elegantly: Our ion pump can just work slowly around the clock to roughly keep the concentration gradient and energy can be supplied slowly for example through ATP-ase, which is already used for many other cell processes. For the channels, no power supply is needed because ions tend to flow toward lower concentration on their own. Making the channels and pump selective to sodium ions (Na⁺) would be a straight-forward choice here as it is already abundant on the outside, which allows for quick and strong amplification through a high concentration gradient.

It is convenient to define the outside potential as 0 as the body of extracellular fluid is so large that ion concentrations are practically constant. This is why the voltage through the membrane (= potential difference between inside and outside) is just called membrane potential.

We are still left with a problem to solve: Once the channels are opened by an above-threshold membrane potential, how do channels know when the signal has passed to close again? Because open channels increase the membrane potential further, we will never get back below the threshold. A simple approach would be to completely inactivate a channel when observing a high membrane potential and de-inactivate it only a while after falling below the threshold, with the delay acting as a buffer to avoid immediate reactivation. We end up with the following hypothetical mechanism:

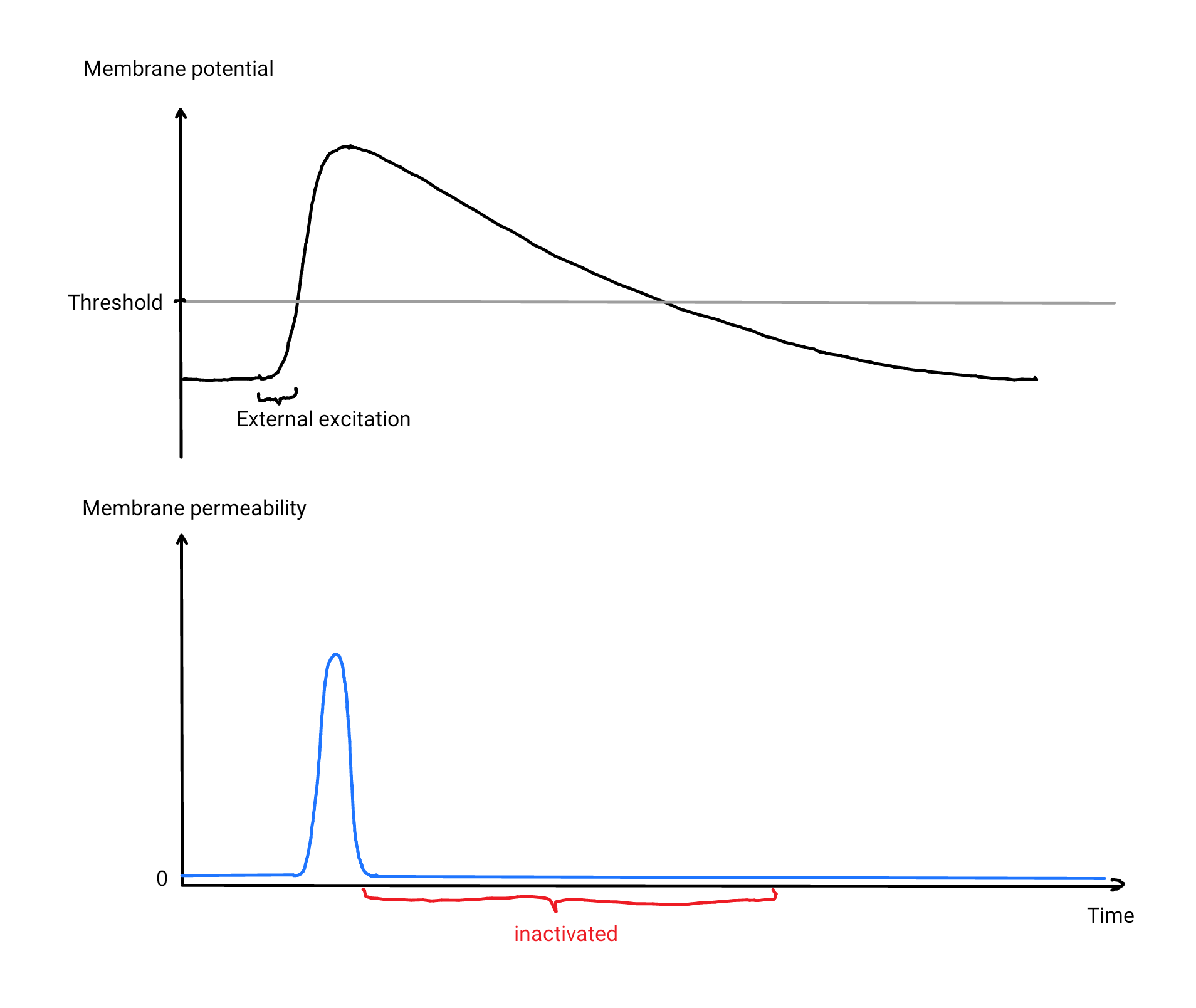
Sodium-only activation

As soon as the membrane potential is raised above the threshold, Na⁺ starts to flood into the fiber, thereby amplifying the membrane potential. After a short time, the channels are inactivated.
Our pumps will slowly bring Na⁺ back out of the cell, which in turn slowly decreases the membrane potential below the threshold and back to its original value (called resting potential).
This causes the channels to be de-inactivated, which makes the fiber ready for the next activation.

In reality, channels do not open for certain at some threshold but instead, they just have a higher probability of opening for higher membrane potentials. \(^{\text{↗ p. 31}}\) Therefore, the permeability of a membrane with large numbers of channels smoothly increases when the membrane potential is raised, although each individual channel is either open, closed or deactivated. We are still not quite there yet, the brain does one more trick:

Improving data rate

The rate at which we can transfer information is proportional to the maximum frequency of activations (and also the accuracy of the spike timing, which is limited by noise). In the mechanism above, this frequency is mainly limited by the slow speed of the sodium pump recovering the resting potential, which makes it necessary to keep Na⁺ channels inactivate for a relatively long time. How can we recover the resting potential faster?

We would need a strong current outwards that is slightly delayed to the inwards current caused by the sodium channels. We used a concentration gradient to quickly move charge into the cell, and it turns out that we can apply the same trick in reverse with the following method: We do not only keep up a low concentration Na⁺ inside the cell with our pump but also build up a concentration gradient for a different ion in reversed direction, with high concentration inside and low concentration outside. To build up this gradient efficiently, it is reasonable to choose an ion that has a low concentration on the outside, such as potassium ions (K⁺), which turn out to be used by the brain for this purpose. If we now add voltage-gated K⁺ channels into the membrane that react more slowly compared to the Na⁺-channels we used before, we end up with the real mechanism \(^{\text{↗ p. 30}}\), carried out by nerve fibers all over your brain in this very moment:

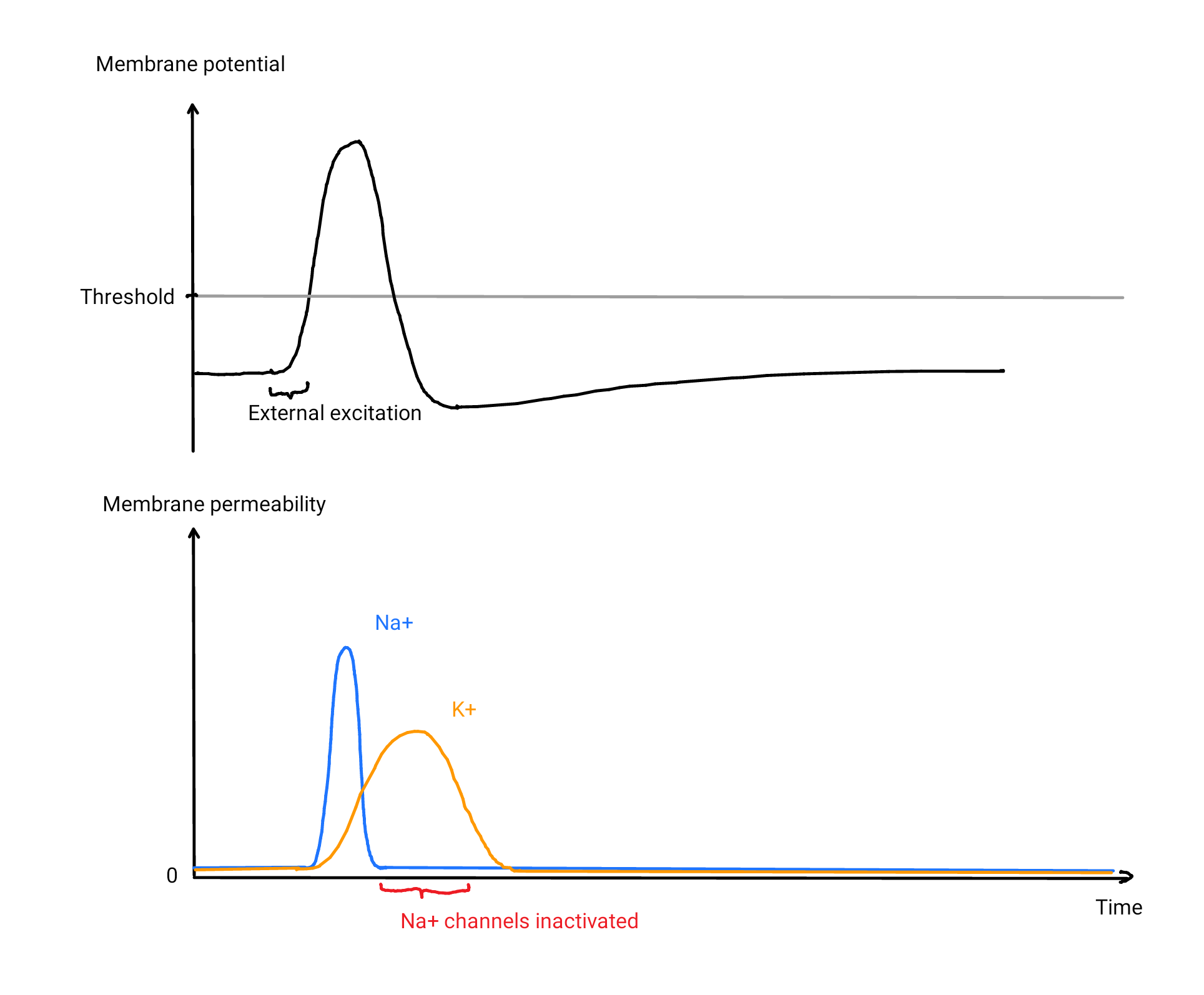
Activation

As soon as the membrane potential is raised above the threshold, Na⁺ starts to flood into the fiber, thereby amplifying the membrane potential. After a short time, the Na⁺-channels are inactivated.
The K⁺-channels open with a delay, and K⁺ flow out of the cell, decreasing the membrane potential rapidly below the threshold. Because of the drop in membrane potential, the K⁺ channels are closed.
The Na⁺-channels are now de-inactivated. Note how we can make the period of inactivation much shorter without the risk of a reactivation loop as we are safely below the threshold very quickly.
Our pumps will bring Na⁺ back out of the cell and K⁺ back inside to make sure the concentrations stay nearly constant. In the brain, both tasks are simultaneously handled by sodium-potassium pumps, which exchange 3 Na⁺ from the inside with 2 K⁺ from the outside. These numbers are somewhat arbitrary, and the mechanism would still work with different ratios.

Because the resulting activation is short, it is also called a spike. In reality, the channels are slightly leaky even if they are closed. This affects the equilibrium concentration, but the mechanism still works in the same way. Nerve fibers are also called axons, and they are a part of (most\(^↗\)) nerve cells, called neurons. In the brain, amplifiers manifest in regular intervals along the axon in form of Ranvier nodes, gaps in the isolation of the otherwise myelinated axon each equipped with many leaky sodium and potassium channels as well as sodium–potassium pumps. There are also unmyelinated axons \(^{\text{↗ p. 32}}\) for information that is not time-critical, with channels and pumps distributed along the way.

Ion concentrations change less than 0.1% during a spike.\(^{↗}\) \(^↗\) Under normal conditions, they never change much more than that, which is why they are assumed to be constant for many calculations.

In summary, we have found an explanation for why we would build axons as they are. These are the key ideas:

Because cells have bad conductance and isolation, amplification is necessary repeatedly for long-range transmission.
The resulting accumulative noise enforces an all-or-nothing encoding.
Na⁺ is actively pumped out to allow for quick passive amplification using Na⁺-channels.
K⁺ is actively pumped in to allow for quick passive recovery using K⁺-channels after an activation, thereby increasing the maximum transmission rate.

Going digital?

Computers use a similar mechanism for transmission as our axons in the brain, only caring about whether a signal is currently present and not about its strength. Computers go a step further though by only caring about whether signals appear in a fixed time window, thereby also discretizing encoding in time. This is achieved through a clock signal, providing the rhythm of processing by defining the boundaries of these time windows. It allows transmitting binary messages, each representing one of two states (commonly called 0 and 1). Multiple of those binary messages can represent arbitrary integers, and thereby encode any discrete message. The absence of analog interpretation of signals and the restriction to discrete-only interpretation is the definition of digital processing. If we make safety margins large enough, both in terms of time and voltage, it is possible to achieve practically error-free transmission. This is a huge benefit, allowing to write complex programs without noise adding up over time (and the reason why we make these strong restrictions in the first place).

In the brain, slow conductors make it hard to have a synchronized clock signal. This rules out digital coding, and we have to deal with noise implied by analog encoding. This means that our brain is restricted to analog coding because the exact timing of each spike influences further processing.

For transmission over short distances we are not constrained to all-or-nothing encoding and in fact amplitude-based encoding is preferable due to higher data rate and energy efficiency. This explains why short neurons never use spikes in the brain.\(^{\text{↗ p. 36}}\) We now understand how and why brain uses a different approach to encode information compared to computers:

Encoding	Discrete voltage	Analog voltage
Discrete timing	digital, used in computers + allows noise-free processing - needs synchronisation, e. g. clock	not used - adds noise through voltage - needs synchronization
Analog timing	used in the brain (axons) + allows long-range transmission even with bad conductors - but then needs energy-costly amplifiers - adds noise through timing	used in the brain (short neurons) - only short-range if conductors bad + high energy efficiency + high data rate - adds noise through timing and strength

Processing

Transistors are the building block for digital processing in computers. How do brains process information? In any case, we need to be able to integrate signals from different sources. Under the assumption that our elemental building block is in our brain is the cell, we would need a structure that allows multiple inputs and multiple outputs. This is what we observe indeed:

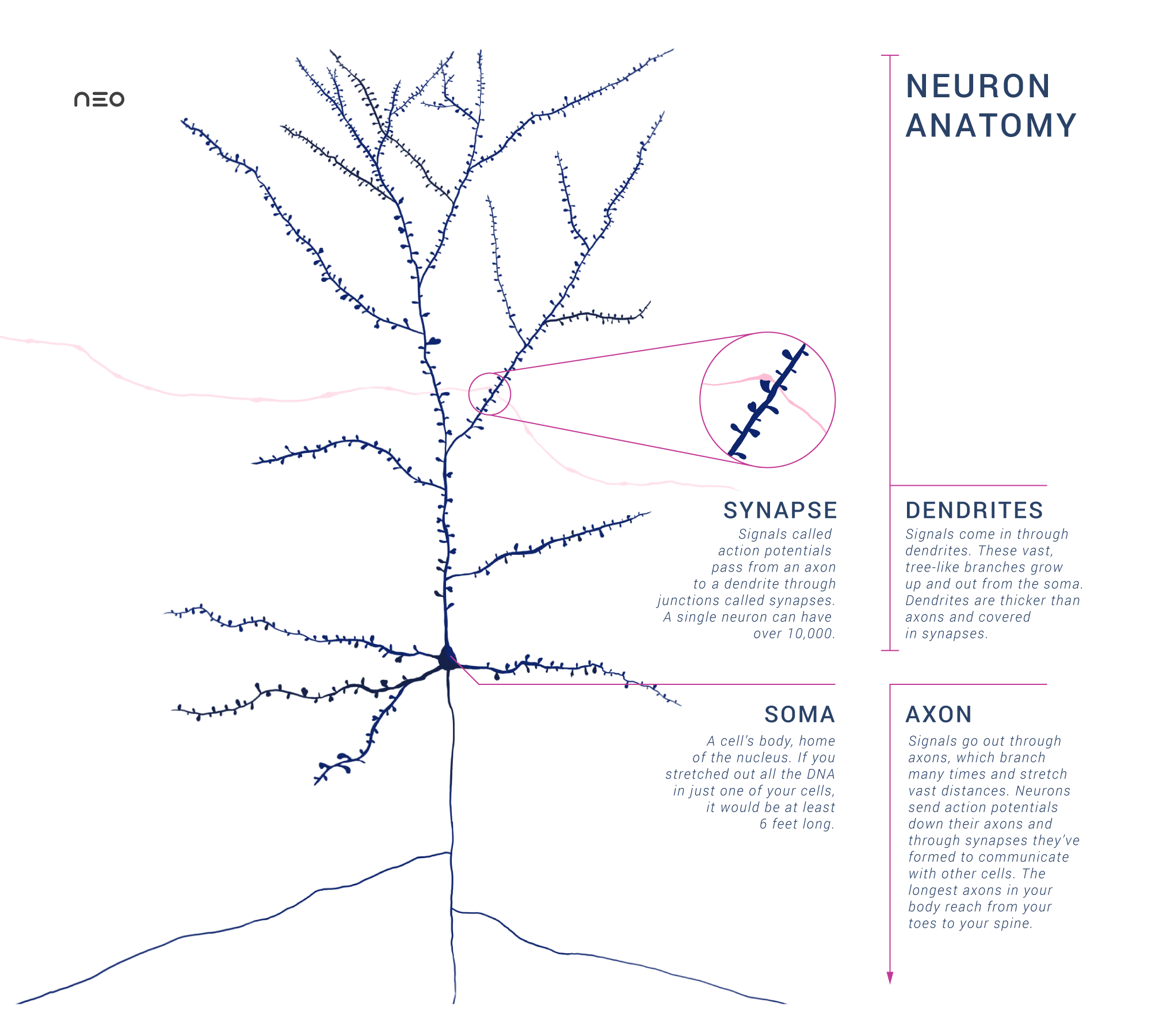
Sodium-only activation

Image created by Amy Sterling and Daniela Gamba licensed under CC BY-SA 4.0

The dendritic tree collects input signals into the soma. When the membrane potential in the soma surpasses a threshold, the axon will transmit a spike, typically also branching to distribute the output signal to other cells at multiple locations.

Dendrites have similarities to axons: Voltage-gated sodium channels open when an input spike arrives, thereby increasing the membrane potential inside the cell. Other than axons, the signal within the dendritic branches is not all-or-nothing, and typically multiple synapses need to be active in order to get the membrane potential in the soma above the threshold. A neuron is “adding up” inputs in some sense, although this is not the complete picture: For example, inputs created by synapses distant from the soma typically have smaller effects. Another example is that if two synapses in one branch fire, the effect is typically different than that of two synapses in different branches. This means that neurons could perform calculations that are far more complex than addition, but it is not yet clear how important this effect is in the brain.

The neuron above is just one type of many, and dendritic and axonal structure as well as the number of synapses vary greatly between types. As described above, short neurons do not even use action potentials.

Designing synapses

How should synapses be designed? A direct conductive connection is arguably the simplest approach. Indeed this observed, especially when reaction time is critical, such as neurons involved in defense mechanisms. The synapse is then called electric synapse, consisting of multiple connecting channels called gap junctions.\(^↗\)

It turns out that this is not the dominant approach and instead, most synapses are chemical:

When a spike arrives at an axon terminal, voltage-gated calcium channels open, and Ca₂⁺ rushes into the cell.
This triggers neurotransmitters to be released, that then passes over to the receiving cell (through the small space in between, called synaptic cleft).
The transmitter bind to receptors, causing sodium channels to open, thereby inducing an increase in membrane potential in the receiving cell.

Why would one use chemical over electric synapses? A big advantage of this mechanism is that it involves chemical receptors on the outside of the receiving neuron allowing for modulation by chemicals broadcasted in the brain. There are many kinds of neurotransmitters and receptors and there are also synapses that inhibit the receiving cell.

Conclusion

There are fundamental questions left unanswered: What information do neurons represent? How do neurons connect to achieve that? How are these representations learned? Neuroscience offers partial answers and algorithmic ideas, but we are far from a complete theory conclusively backed by observations.

Nevertheless, we saw the reasons behind some fundamental design choices that make your brain work.